2018は7から18までの連続した整数の自乗和らしいので、似たような現象がこの先いつあるか調べてみた-完全版

前回の記事はこちら↓。
2018は7から18までの連続した整数の自乗和らしいので、似たような現象がこの先いつあるか調べてみた-前編

その後考えてみたら、むしろ少ない数の連続した整数になるほうが興味深いといことに気づいた。
と言うか、結果を見れば一目瞭然なのだが、

2018 = 7^2 + 8^2 + 9^2 + … + 18^2
のとき、
2054 = 6^2 + 7^2 + 8^2 + 9^2 + … + 18^2
2079 = 5^2 + 6^2 + 7^2 + 8^2 + 9^2 + … + 18^2
…
2109 = 1^2 + 2^2 + 3^3 + … + 18^2
なんて、あたりまえじゃないか。

ということで、この調査では、連続した整数の個数が少ないほうが価値が高い。
そこで、前回紹介したマクロを、以下のようにマクロを改変した。

以下のマクロは、まっさらなシートを2つ用意し、それぞれ、「Check」、「Result」という名称にして実行する。

'事前にシート「Check」とシート「Result」を用意すること
Sub CalcJijyowa()
    Worksheets("Check").Activate
    Dim cTate As Long
    Dim cYoko As Long
    For cTate = 1 To 34
        Range("A1").Offset(cTate).Value = cTate
    Next
    For cYoko = 2 To 19
        Range("A1").Offset(, cYoko - 1).Value = cYoko
    Next
    
    Dim cSum As Long
    Dim cNum As Long
    Dim cTgt As Long
    For cNum = 8 To 8 + 12 - 1
        cSum = cSum + cNum ^ 2
    Next
    cTgt = cSum
    
    Dim cList As Long
    Dim wList As Worksheet
    Set wList = Worksheets("result")
    cList = 2
    For cYoko = 2 To 19
        For cTate = 1 To 34
            cSum = 0
            For cNum = cTate To cTate + cYoko - 1
                cSum = cSum + cNum ^ 2
            Next
            Range("A1").Offset(cTate, cYoko - 1).Value = cSum
            If cSum >= 2018 And cSum <= cTgt Then
                Range("A1").Offset(cTate, cYoko - 1).Font.Color = vbRed
                Range("A1").Offset(cTate, cYoko - 1).Font.Bold = True
                wList.Range("L" & cList).Value = cTate & "から"
                wList.Range("M" & cList).Value = cYoko & "個連続"
                wList.Range("N" & cList).Value = cSum
                cList = cList + 1
            End If
            If cSum >= cTgt Then
                Exit For
            End If
        Next
    Next
    wList.Range("L1").Value = "最初の数字"
    wList.Range("M1").Value = "自乗回数"
    wList.Range("N1").Value = "合計値"
    wList.Range("L1").CurrentRegion.Sort Key1:=wList.Range("N1"), Order1:=xlAscending, Header:=xlYes
    For cNum = 2 To cList - 1
        Debug.Print wList.Range("L" & cNum).Value & " " & wList.Range("M" & cNum).Value & " : " & wList.Range("N" & cNum).Value
    Next
End Sub

その結果は、以下のとおり。

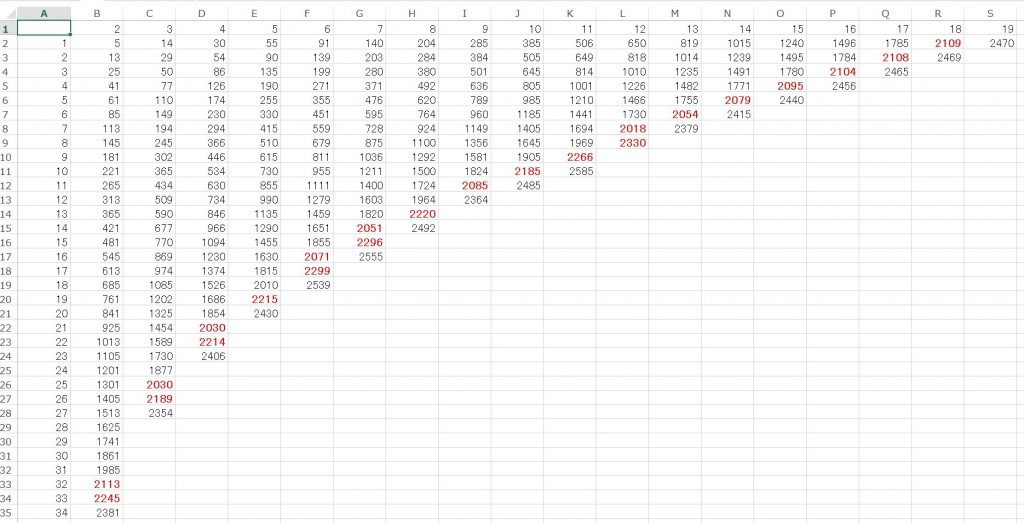
2018は7から連続した12個の数値の自乗和らしいので、似たような現象がこの先いつあるか調べてみた。その結果。(完全調査バージョン)

出力結果は以下のとおり。
7から 12個連続 : 2018
25から 3個連続 : 2030
21から 4個連続 : 2030
14から 7個連続 : 2051
6から 13個連続 : 2054
16から 6個連続 : 2071
5から 14個連続 : 2079
11から 9個連続 : 2085
4から 15個連続 : 2095
3から 16個連続 : 2104
2から 17個連続 : 2108
1から 18個連続 : 2109
32から 2個連続 : 2113
10から 10個連続 : 2185
26から 3個連続 : 2189
22から 4個連続 : 2214
19から 5個連続 : 2215
13から 8個連続 : 2220
33から 2個連続 : 2245
9から 11個連続 : 2266
15から 7個連続 : 2296
17から 6個連続 : 2299
8から 12個連続 : 2330

2030年の、「25から3個連続」かつ、「21から4個連続」は興味深い。
最も少ないのは、2113年の、「32から2連続」→32^2 + 33^2。これは、奇しくも、ドラえもんの生まれる前年ですね。まさか、藤子不二雄は狙っていたわけではあるまい。

連続する整数の数が少ない順に並べると以下のとおり。

32から 2個連続 : 2113
33から 2個連続 : 2245
25から 3個連続 : 2030
26から 3個連続 : 2189
21から 4個連続 : 2030
22から 4個連続 : 2214
19から 5個連続 : 2215
16から 6個連続 : 2071
17から 6個連続 : 2299
14から 7個連続 : 2051
15から 7個連続 : 2296
13から 8個連続 : 2220
11から 9個連続 : 2085
10から 10個連続 : 2185
9から 11個連続 : 2266
7から 12個連続 : 2018
8から 12個連続 : 2330
6から 13個連続 : 2054
5から 14個連続 : 2079
4から 15個連続 : 2095
3から 16個連続 : 2104
2から 17個連続 : 2108
1から 18個連続 : 2109

そろそろ出かけないと、天皇杯の横浜マリノス-セレッソ大阪戦の前に現地でゆっくりできなくなってしまうので、これにて。

前回の記事はこちら↓。
2018は7から18までの連続した整数の自乗和らしいので、似たような現象がこの先いつあるか調べてみた-前編